A. KOMPETENSI DASAR:

3.6 Menjelaskan dan membuktikan teorema Pythagoras dan tripel Pythagoras.
4.6 Menyelesaikan masalah yang berkaitan dengan teorema Pythagoras dan tripel Pythagoras.

B. PETA KONSEP

C. KEGIATAN 6.1 MEMERIKSA KEBENARAN TEOREMA PYTHAGORAS

Teorema Phytagoras merupakan seuah aturan matematika yang bisa dipakai dalam menentukan panjang salah satu sisi dari suatu segitiga siku-siku.

Yang perlu kalian ingat dari teorema Pythagoras yaitu teorema hanya berlaku untuk segitiga siku-siku. Maka dari itu tidak dapat digunakan untuk menentukan sisi dari sebuah segitiga lain yang tidak berbentuk siku-siku.

Teorema pythagoras masuk ke dalam salah satu materi dalam mata pelajaran matematika dasar yang mempunyai perluasan serta manfaat yang sangat banyak.

Pembuktian teorema Pythagoras berkaitan erat dengan luas persegi dan segitiga. Pythagoras telah mengungkapkan bahwa kuadrat panjang sisi miring suatu segitiga siku-siku sama dengan jumlah kuadrat panjang sisi-sisi yang lain. Untuk memeriksa kebenarannya, silahkan amati pada video berikut!

D. MENGIDENTIFIKASI SEGITIGA SIKU-SIKU

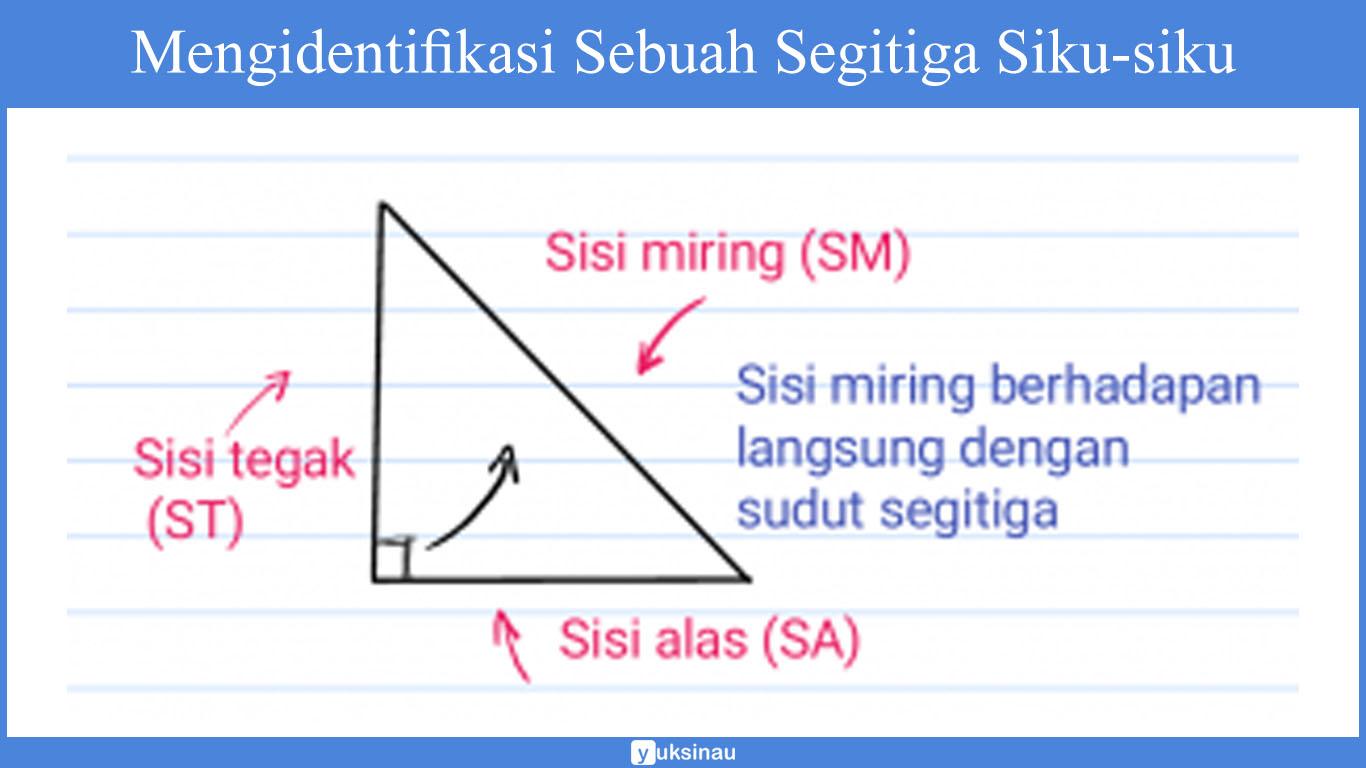
Pada segitiga siku-siku, Sisi miring segitiganya berhadapan langsung dengan sudut siku-siku dari segi tiga di atas

E. Rumus Teorema Pythagoras

Teorema ini pertama kali dikemukakan oleh seorang matematikiawan yang berasal dari Yunani bernama Phytagoras.

Adapun bunyi atau dalil Teorema Phytagoras yaitu sebagai berikut:

Pada suatu segitiga siku-siku, kuadrat dari sisi terpanjang yaitu sama dengan hasil jumlah dari kuadrat sisi-sisi penyikunya.

Dari teorema tersebut bisa kita bikin suatu rumus yang bisa kita gambarkan seperti di bawah ini:

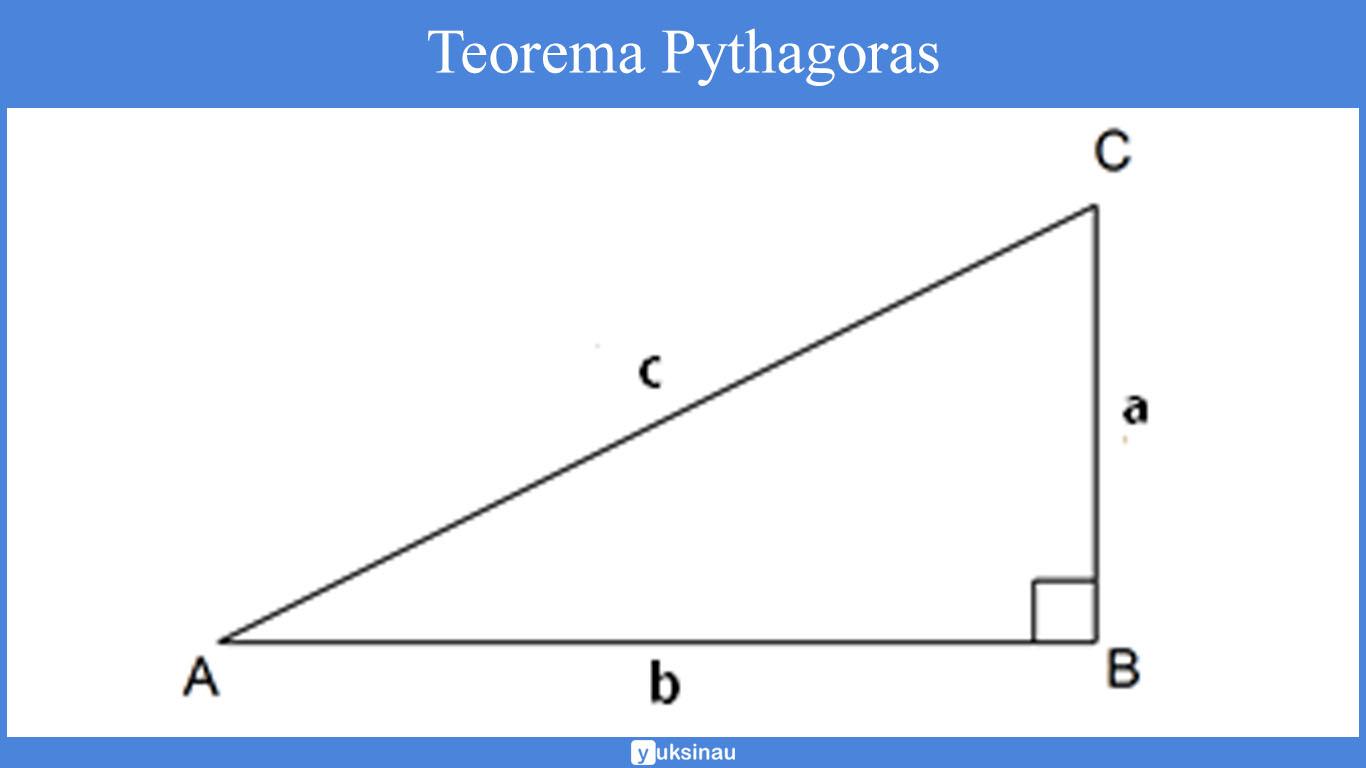
Rumus Phytagoras

c² = a²  + b²

Keterangan:

c = sisi miring
a = tinggi
b = alas

F. Kegunaan Dalil Teorema Phytagoras

1. Menentukan Panjang Sisi Segitiga

Secara matematis, rumus dari Phytagoras biasa dipakai untuk menentukan panjang sisi dari suatu segitiga siku-siku.

Untuk lebih jelasnya, perhatikan beberapa contoh soal di bawah ini.

Contoh Soal Pythagoras (Pitagoras) dan Penyelesaiannya

Soal 1.

Diketahui segitiga siku-siku ABC dengan siku-siku di B yang digambarkan sebagai berikut:

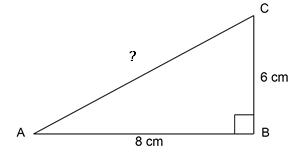
Tentukan panjang sisi miring AC pada gambar di atas!

Jawab:

Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti betikut ini:

AC² = AB² + BC²
AC² = 8² + 6²
AC² = 64 + 36
AC² = 100
AC  =  √100
AC  = 10

Sehingga, panjang sisi AC dalam segitiga siku-siku tersebut yaitu 10 cm.

Soal 2.

Suatu segitiga siku-siku KLM dengan siku-siku di L digambarkan seperti di bawah ini:

Tentukan panjang sisi KL pada gambar di atas!

Jawab:

Sebab, segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti berikut ini:

KM² = KL² + LM²
KL² = KM² – LM²
KL² = 13² – 12²
KL² = 169 – 144
KL² = 25
KL  =  √25
KL = 5

Sehingga, panjang sisi KL dalam segitiga siku-siku di atas yaitu 5 cm.

Soal 3.

Diketahui segitiga siku-siku DEF dengan siku-siku di E digambarkan seperti di bawah ini:

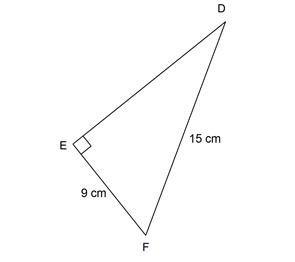
Tentukan panjang sisi DE pada gambar di atas!

Jawab:

Sebab segitiga DEF di atas merupakan segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:

DF² = DE² + EF²
DE² = DF² – EF²
DE² = 15² – 9²
DE² = 225 – 81
DE² = 144
DE  =  √144
DE = 12

Sehingga, panjang sisi DE pada segitiga siku-siku di atas yaitu 12 cm.

Soal 4.

Diketahui segitiga siku-siku ABC dengan siku-siku berada di B. Apabila panjang sisi AB = 16 cm serta Panjang sisi BC = 12 cm.

Maka hitunglah panjang sisi AC pada segitoga di atas!

Jawab:

Dari soal di atas bisa kiat gambarkan sebuah segitiga siku-siku seperti berikut ini:

Sebab segitiga di atas adalah segitiga siku-siku, maka berlaku rumus Phytagoras seperti di bawah ini:

c² = a²  + b²
c² = 12² + 16²
c² = 144 + 256
c² = 400
c = √400
c = 20

Sehingga, panjang sisi AC pada segitiga siku-siku ABC dalam soal di atas yaitu 20 cm.

2. MENENTUKAN JARAK 2 TITIK

Jarak dua buah titik pada bidang koordinat bisa ditemukan dengan bantuan rumus pitagoras. Kedua titik itu akan saling membentuk segitiga siku-siku.

Soal :

1. Hitunglah jarak yang dibentuk oleh titik A (3,1) dan B (7,4)!!

Untuk menghitung jarak x dan y, kita harus membuat dulu titik-titik yang sudah diketahui dan memecahnya.

Titik A (3,1) :

• x₁ = 3
• y₁ = 1

Titik B (7,4) :

• x₂ = 7
• y₂ = 4

Jarak titik A dan B kita misalkan AB dan dihitung menggunakan rumus pitagoras dengan AB sebagai sisi miring.

AB² = x² + y²

• x = 4
• y = 3

AB² = 4² + 3²
AB² = 16 + 9
AB² = 25
AB = √25
AB = 5

Jadi jarak antara titik A dan B adalah 5 satuan.

3. Menentukan panjang diagonal kubus dan Balok

1. Menentukan panjang diagonal persegi

Contoh soal: 

Sebuah persegi ABCD mempunyai panjang 8 cm dan lebar 6 cm. Tentukanlah panjang diagonal dari persegi tersebut.

Jawab: 

Diketahui:

• panjang = p = 8 cm
• lebar = L = 6 cm

Ditanya:

• diagonal = d = … ?

Berdasarkan dalil Pythagoras, maka:

⇒ d² = p² + L²
⇒ d² = 8² + 6²
⇒ d² = 64 + 36
⇒ d² = 100
⇒ d = √100
⇒ d = 10 cm

Sehingga, panjang diagonal persegi pada soal di atas adalah 10 cm

2. Menentukan diagonal ruang kubus dan juga balok

Diberikan suatu balok ABCD.EFGH seperti yang terlihat pada gambar di bawah ini:

Contoh soal: 

Suatu balok memiliki panjang, lebar, dan tinggi berturut-turut yaitu 12 cm, 9 cm, dan 8 cm. Tentukanlah panjang salah satu diagonal ruangnya!

Jawab: 

Diketahui:

• p = 12 cm
• L = 9 cm
• t = 8cm

Ditanya:

• d_r = … ?

Berdasarkan dari bunyi atau dalil Pythagoras, maka:

⇒ d_r² = p² + L² + t²
⇒ d_r² = 12² + 9sup>2 + 8²
⇒ d_r² = 144 + 81 + 64
⇒ d_r² = 289
⇒ d_r = √289
⇒ d_r = 17 cm

Sehingga, panjang diagonal ruangnya yaitu 17 cm.

~:: TUGAS PERTEMUAN 1::

Petunjuk!!
Kerjakan Tugas di bawah di Buku Tulis dengan menuliskan nama lengkap dan kelas. Un6uk pengumpulan Tugas selain melalui Google Classroom, juga di kumpulkan ke sekolah dalam bentuk Portofolio, sehingga harus di tulis di buku/kertas

____________________________

SOAL

____________________________

1. Perhatikan gambar berikut!

Hitunglah panjang PQ

2. Hitunglah jarak yang dibentuk oleh titik A (-2,3) dan B (4, -1)!!

3. Perhatikan Balok ABCD.EFGH berikut!

Tentukan panjang AG