MENENTUKAN AKAR PERSAMAAN KUADRAT DENGAN RUMUS ABC

Perhatikan bentuk umum dari persamaan kuadrat berikut.
ax² + bx + c = 0 dengan a merupakan koefisien dari x² dimana a , b meruakan koefisien dari x dan c merupakan konstanta. Dalam rumus kuadrat ketiga angka tersebut diperlukan

Rumus kuadrat atau rumus abc merupakan penurunan dari cara melengkapkan kuadrat sempurna. Dengan cara melengkapkan kuadrat sempurna kita dapat menemukan rumus kuadrat tersebut. Penurunan rumus kuadrat tersebut dijabarkan sebagai berikut.
ax² + bx + c = 0
Bagi kedua ruas dengan a agar koefisien x² bernilai 1 hal ini dilakukan agar kita dapat dengan mudah menggunakan cara melengkapkan kuadrat sempurna

Berdasarkan uraian di atas didapat rumus untuk mendapatkan akar-akar persamaan
kuadrat atau biasanya disebut sebagai rumus kuadratik/rumus abc yaitu

Nilai diskriminan ini mempengaruhi penyelesaian/akar-akar dari persamaan kuadrat.

1. Jika b² – 4ac = 0, maka persamaan kuadrat tersebut memiliki satu selesaian bilangan real yang sama (kembar)
2. Jika b² – 4ac > 0, maka persamaan kuadrat tersebut memiliki dua selesaian bilangan real yang berbeda.
3. Jika b² – 4ac < 0, maka persamaan kuadrat tersebut tidak memiliki akar real (akarnya imajiner).

Dari persamaan kuadrat berikut, tentukan jenis akar persamaan kuadrat berdasarkan nilai diskriminannya

CONTOH

1. Tentukan akar-akar persamaan kuadrat 2x² – 4x – 3 = 0 dengan menggunakan rumus kuadrat!

Penyelesaian:

2x² – 4x – 3 = 0
Dari persamaan di atas didapat nilai a = 2, b = -4 dan c = -3. Kemudian kita masukkan nilai a, b, dan c ke dalam rumus kuadrat maka,

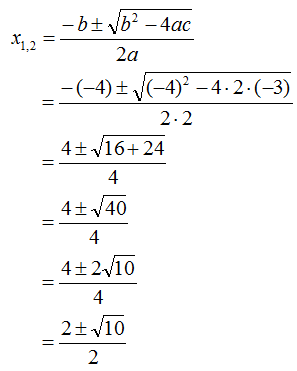
Jadi, akar-akar persamaan 2x² – 4x – 3 = 0 adalah

~::TUGAS::~

kerjakan soal berikut di buku tugas kalian (tuliskan nama lengkap dan no Presensi), kemudian Foto dan Upload google classroom kalian

1. Dengan melengkapkan menjadi kuadrat sempurna tentukan akar persamaan kuadrat dari

2. Tentukan nilai diskriminan dari persamaan kuadrat berikut!

3. Dengan rumus abc, tentukan akar persamaan kudrat dari: